在 Android 中实现 iOS 液态玻璃效果
探索
苹果是如何实现液态玻璃的呢? 大体思路是这样的:给定一个形状,获取该形状的内边界,即玻璃效果开始的边界,然后从内边界到外边界过渡,就像等高线图一样。由任意点的过渡值(从 0 到 1)可以实现各种效果,比如位移、颜色混合等。
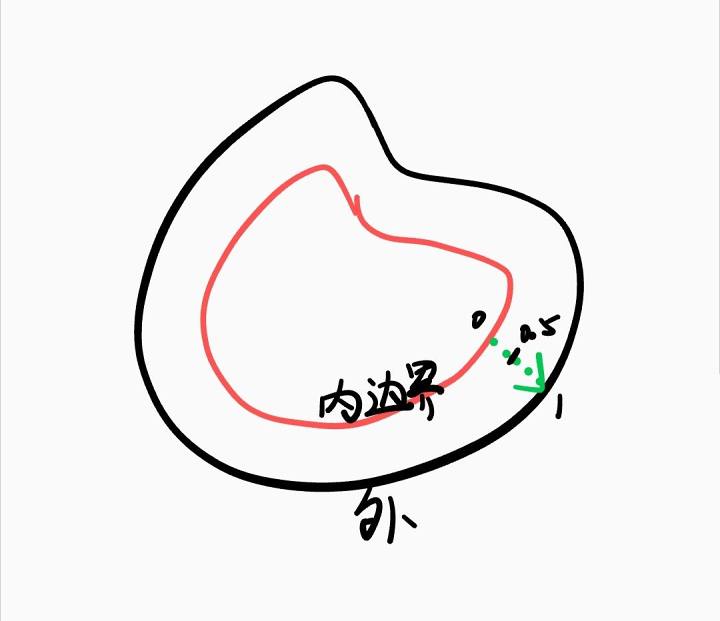
但是只知道过渡值是不够的,我们还要知道任意点到边界的哪个点距离最小。没错,上文中的过渡值就可以表示该点到边界的最小距离,距离除以长度就是过渡值。
划重点!!
因此我们明确了要找两样东西:
- 🤩 任意点到边界的最小距离
- 🤗 任意点到边界的哪个点距离最小 为了寻找 🤩,我们引入小学三年级学习过的 SDF
有符号距离场 (SDF, signed distance field)
有符号距离场(或有符号距离函数),用于描述任意点到某个形状边界的最短距离,并附带符号信息以区分点是在图形内部还是外部。一般规定点在形状内部符号为负。
它就像一个地形图:
- 我围一块地,离地的边界越远,SDF 距离的绝对值越大
- 地的外面是海洋,海拔为负,SDF 为正;地的里面是陆地,海拔为正,SDF 为负

圆角矩形的 SDF
这里我们使用二维距离场,用 f(x, y) 表示。并且只关心形状内部。
我们先看中心在原点、半径为 R 的圆的距离场:
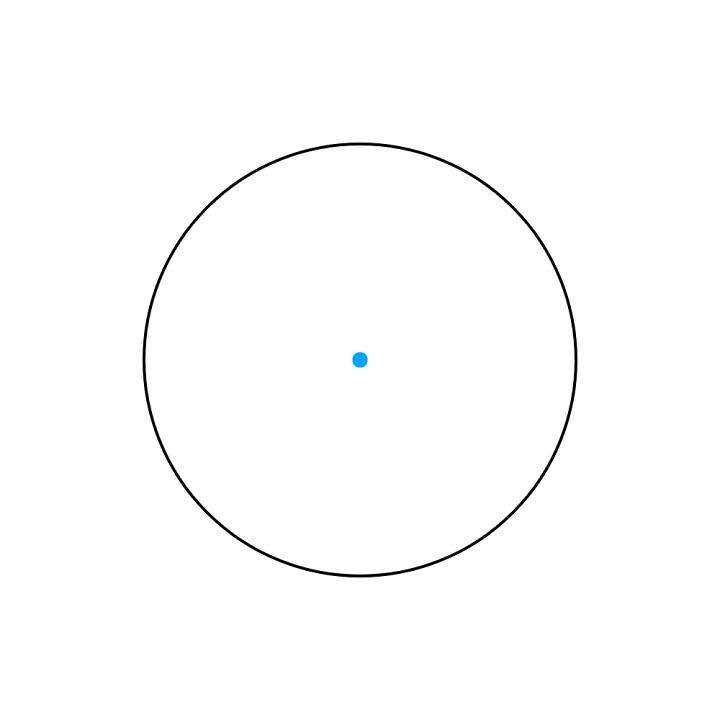
先看中点,很明显 f(0, 0) = -R,注意符号 那么在任意点 P 呢?
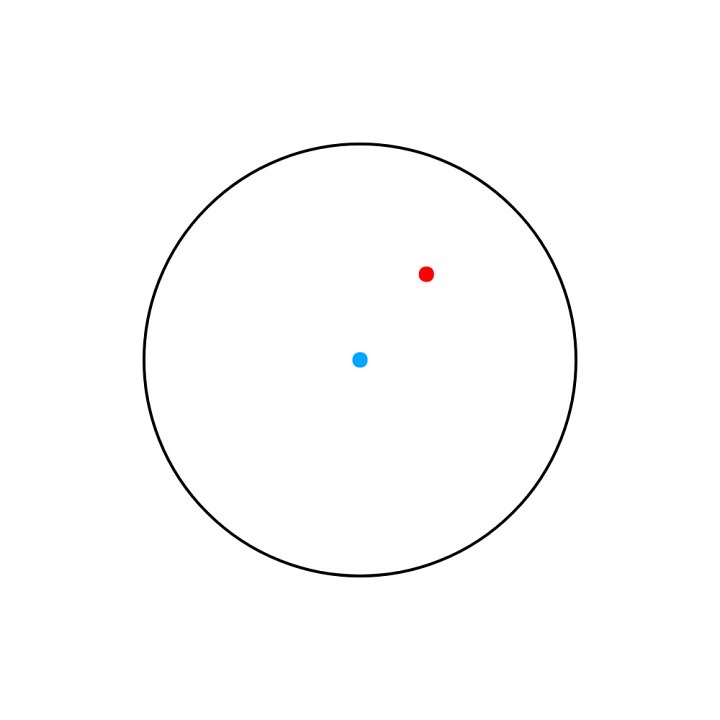
答案是,从原点出发经过点 P 的射线,与圆有一交点,该交点到点 P 的距离最短,且距离为 R - √(x²+y²)
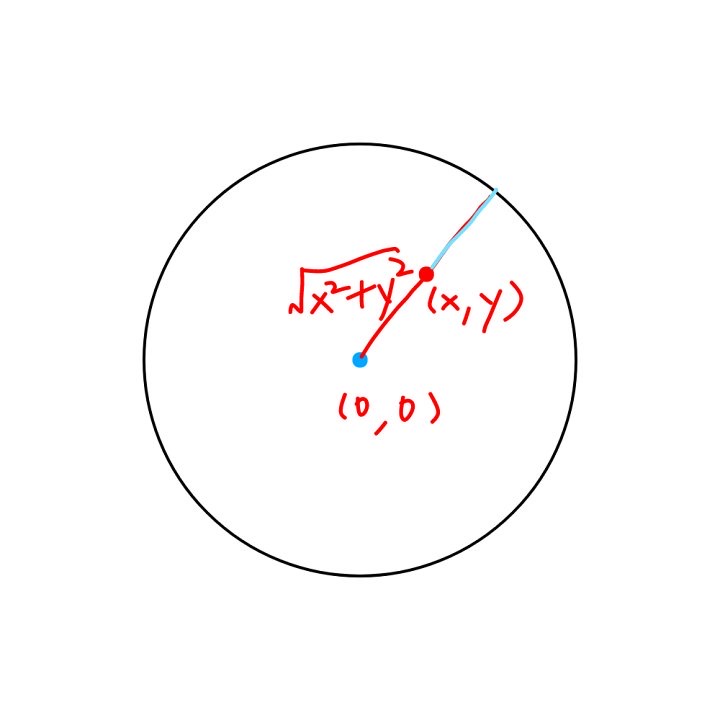
在形状的内部符号为负,实际的 f(x, y) = √(x²+y²) - R,在原点处也成立。
再看中心在原点、横纵长度为 a, b 的矩形的距离场:
我相信你们已经不想看了,在此略过。
最后看圆角矩形的距离场:
把一个矩形向外扩展,并保持新边界与原边界的距离不变,就能得到一个圆角矩形:

将该过程逆转,即缩小圆角矩形得到一个无圆角的矩形。如果矩形的距离场为 f,那么圆角为 r 的矩形的距离场为 f - r,非常的 啊 mazing 啊! 该公式对任意形状都成立。 更多的距离场可在这里查询:[查看链接] 知道了 SDF (🤩),还要知道另一个东西 🤗:
梯度 (Gradient)
我们小学二年级就学过的,梯度是函数在空间中某一点的方向导数向量,表示在该点距离值变化最快的方向。它在几何上等价于该点所在的最短距离方向向量。一般用 grad 表示。没错,他就是我们要找的 🤗。归一化后的 SDF 的梯度就是边界法线的方向。 他跟导数很像,不过是带方向的导数。
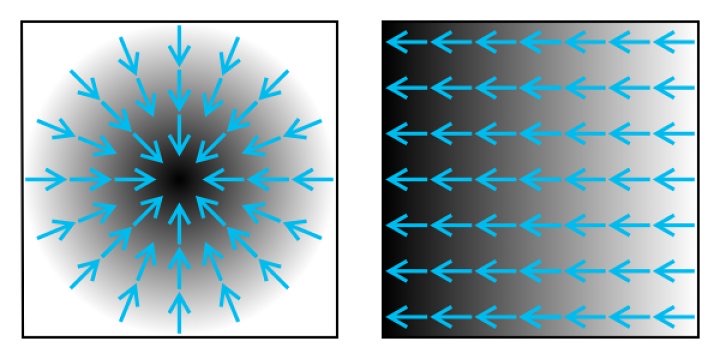
万幸的是我们目前的 SDF 都是解析的,你可以理解为可以输入无限的坐标值,包括小数。因此很容易计算出梯度的精确值: 取一个小值 ε,已知某一点 P 的 SDF 为 f(x, y),在点 P 的梯度(未归一化)
grad(x, y) = [f(x+ε, y)-f(x-ε, y)] + [f(x, y+ε)-f(x, y-ε)]说点通俗易懂的吧:
在地形图中,地形高度就是 SDF 距离值,假设我在地上放置一个小球,小球的滚动方向就是梯度。 话说我们是不是可以把 SDF 和梯度结合起来,叫”方向距离场”?它会是一个向量场,幅值表示最小距离 🤩,方向表示该点梯度 🤗
Shader 实现思路
- 输入矩形大小、中点、圆角值 r、玻璃边缘大小 t
- 计算圆角矩形的 SDF
- 如果像素点的 SDF 在 (-t, 0),进行如下操作,否则返回原像素
- 将中心点减去 SDF 的绝对值,得到相对于玻璃边缘内边界的无符号距离 d
- 计算该点的梯度,目的是寻找法线方向
- 折射:沿着梯度的反向变换坐标
- 细节处理:iOS 26 不仅仅有梯度方向的折射,还有额外效果:

看到即使梯度方向垂直,但是会向左/右弯曲的线了吗,这里也要处理。
实现效果
我实现的 shader 一共 54 行代码,效果如下: